The Momentum indicator supports traders to assess the market trend continuation and trend reversals. The momentum indicator often moves according to the price action and occasionally diverges from the price trend of the underlying traded instrument. The divergence is a powerful signal to identify and anticipate trend reversals. The momentum indicator formula is quite simple yet powerful. It consists of the latest price subtracted by the closing price of the specified number of periods ago.

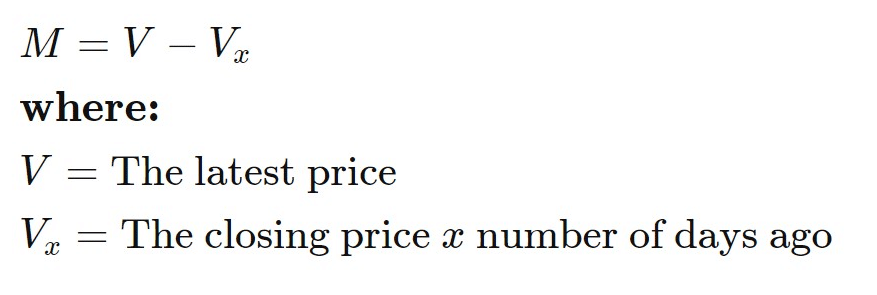
Fig.222 Momentum indicator formula

In this guide, we will go over the details of how to define the entry based on the divergence between the traded instrument price action and the Momentum indicator. We will also go through the process of storing the indicator data points and how to retrieve them to create a simple trend reversal trading strategy. There is a critical difference between MQL4 and MQL5; the MQL4 Momentum function retrieves the indicator’s data point, while MQL5, on the other hand, returns the indicator handle. 

MQL5 requires the data to be stored in the indicator buffer, which requires a double type array to be declared. It may seem difficult to understand at first, however, the concept is quite simple. We will go into the details step by step and will demonstrate a practical example of usage with code ready to use.

How does the Momentum indicator works?

Before we go through the details of the Momentum indicator code implementation, let us explain the entry signals interpretation. Note that it is recommended to use the Momentum indicator strategy in combination with another indicator. 

The Momentum indicator is very effective in determining potential price reversal for entry signals. However, we suggest the use of another indicator to define exit signals. It is an unbound oscillator, which means that the upside and downside level has no limits, hence the indicator may not allow the trader to identify overbought or oversold territories subjectively. 

One of the most powerful approaches to use this indicator is to detect divergence between the indicator and the price action. Often, divergence occurs before trend reversals. A bullish reversal happens when the underlying instrument’s price action is in a downward slope while the Momentum indicator is rising (Fig.223). Conversely, a bearish reversal occurs when the traded instrument’s price action is on an upward slope while the Momentum indicator is declining, which may signal a fading bullish trend and an imminent trend reversal.

Fig.223 Momentum indicator: Divergence pattern

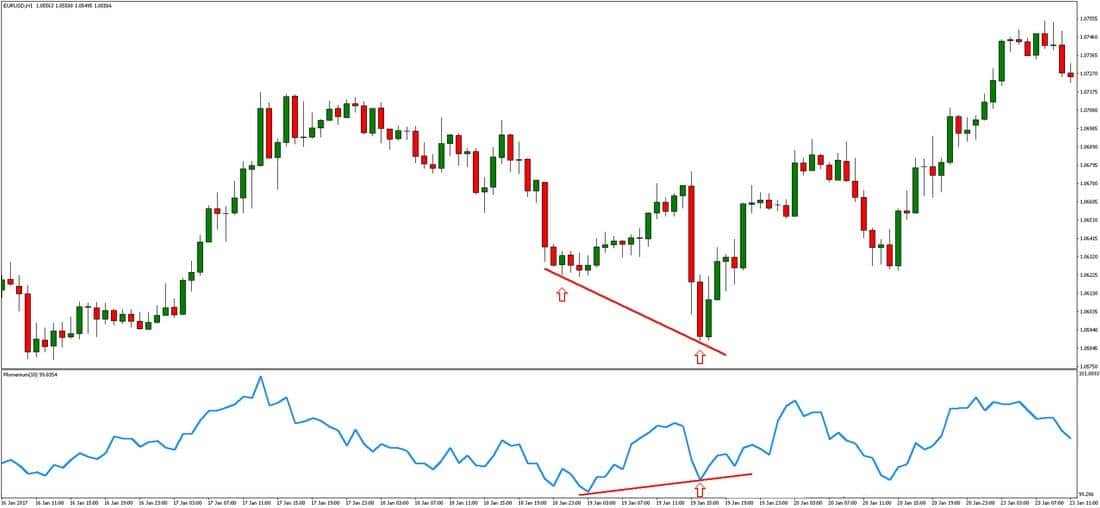
How does the Momentum indicator store data points?

The Momentum indicator stores its data point in an indicator buffer which is automatically initiated by Metatrader. It is a dynamic array that loads during the Expert Advisor initialization. An indicator buffer is a time-series array; hence, it has the distinction of reverse indexing. It implies that the array is sorted from the most recent data point to the oldest data point. A time-series array contains date and time information.

The time-series element with index zero contains the latest quote of a symbol. As an example, an indicator on the daily timeframe will have the current data point at index zero and yesterday’s data at the position index one (Fig.224).

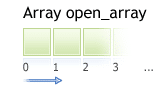
Fig.224 Indicator data points array

MQL5

To get the Momentum indicator data, MQL5 requires the use of the CopyBuffer() function. This method does not apply to MQL4 as the MQL4 indicators function immediately returns the value of the iMomentum data point instead of the indicator handle. The following parameters should be provided:

1. Specify the handle that is returned by the iMomentum() function.
2. Provide the buffer number. You may provide zero as the default value.
3. Provide the start position. You may specify zero to retrieve from the most recent data point. This number characterizes the index where zero is the most recent data point, and one is the previous data point.
4. Specify the number of data points to get from the iMomentum() function.
5. Provide the variable where the data will be stored. The variable is a double type.

How to retrieve the Momentum indicator data with the CopyBuffer() function?

1. Declare a variable for the handle: int IndicatorHandle = iMomentum();
2. Declare a variable to store indicator data: double mom_indicator;
3. Copy the data to the indicator variable and retrieve data points
   1. CopyBuffer(IndicatorHandle, 0, 0, 100, mom_indicator);
   2. Retrieve iMomentum data point with mom_indicator[0], mom_indicator[1].

Fig.225 CopyBuffer() Function

How to access the indicator data?

MQL4

The iMomentum() function will return the indicator data point according to these five parameters:

1. The symbol of the traded instrument. You may provide a string such as “EURUSD” or use the function Symbol() to retrieve the symbol from the chart where the Expert Advisor is attached.
2. Provide the time frame using the enumeration value from the constant ENUM_TIMEFRAMES, for instance:
   1. PERIOD_CURRENT, for the current timeframe from the chart,
   2. PERIOD_M1, for the one-minute timeframe,
   3. PERIOD_D1, for the daily timeframe.
3. Specify the averaging period. Usually, the Momentum indicator is a 14-period.
4. Provide the applied price method by specifying an enumeration value from the constant ENUM_APPLIED_PRICE, for instance:
   1. PRICE_CLOSE, for close price
   2. PRICE_OPEN, for open price
   3. PRICE_HIGH, for the highest price in the specified period
   4. PRICE_LOW, for the lowest price in the specified period
5. Provide the index of the indicator buffer where zero is the last data point and one the previous data point.

Fig.226 MQL4 Momentum function

MQL5

When calling the iMomentum() function, the function will create the Momentum indicator in the MetaTrader global cache and returns its handle according to the following parameters:

1. The symbol of the traded instrument. You may specify a string such as “EURUSD” or you can use the function Symbol() to get the symbol from the chart where the Expert Advisor is attached.
2. The time frame of the data point to extract using the enumeration value from the constant ENUM_TIMEFRAMES:
   1. PERIOD_CURRENT, to get data points from the current timeframe from the chart to which the Expert Advisor is attached,
   2. PERIOD_M1, for the one-minute timeframe,
   3. PERIOD_D1, for the daily timeframe.
3. The averaging period. Usually, the Momentum indicator default value is 14-period.
4. Provide the applied price method using the ENUM_APPLIED_PRICE constant, for instance:
   1. PRICE_CLOSE, for the close price,
   2. PRICE_OPEN, for the open price,
   3. PRICE_HIGH, for the highest price within the specified period,
   4. PRICE_LOW, for the lowest price within the specified period.

Note that to retrieve data points from the iMomentum() function, you need to use it in combination with the function CopyBuffer().

Fig.227 MQL5 Momentum function

Practical case

MQL5

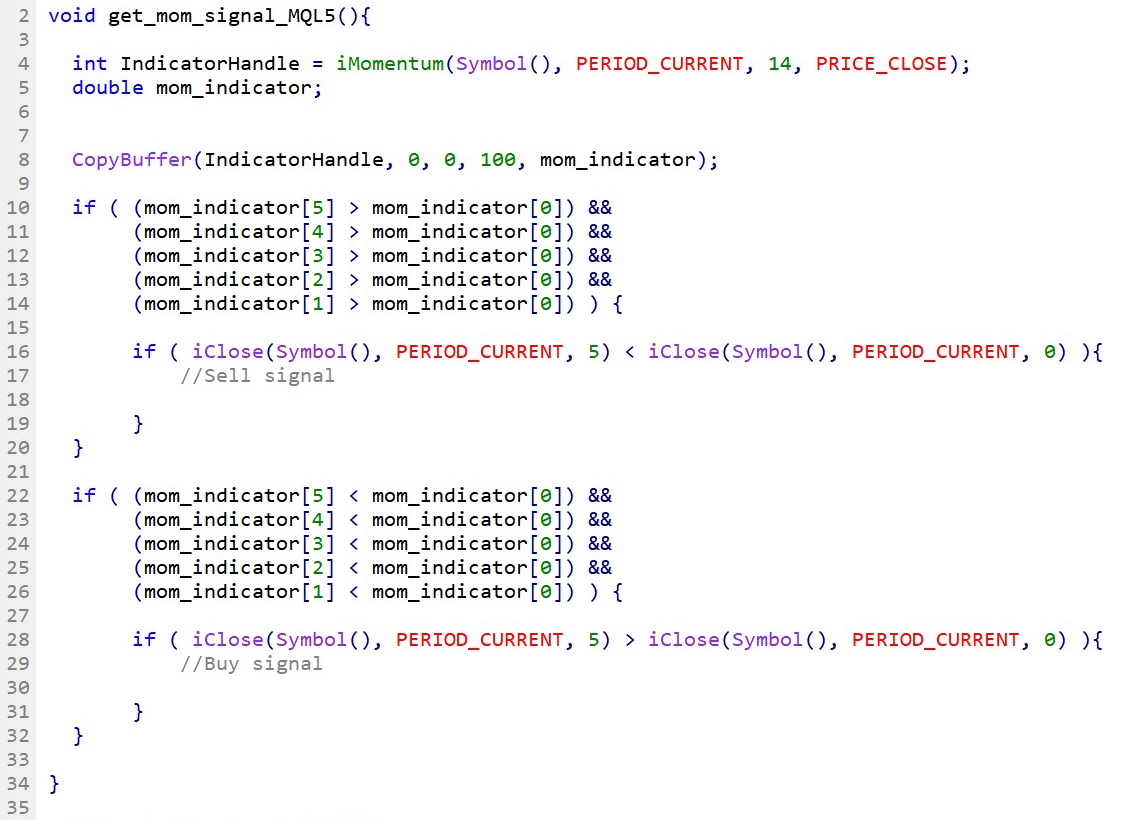
Fig.228 illustrates the use of the Momentum indicator to identify price reversal from a divergence between the unbounded oscillator and the price action. 

Line 4: Declare the indicator handle and assign specified parameters to the iMomentum() function handle.

Line 5: Declare the indicator as a double type array to store the iMomentum indicator data points.

Line 8: Save the last hundred data points from the buffer into the indicator array mom_indicator.

Line 10 – 32: IF statement to find divergence by comparing the last 5 data points with the latest data point to identify the Momentum indicator slope. Compare as well the underlying instrument’s price action to determine the trend. A signal is materialized when the momentum indicator and the price action trend move in the opposite direction.

Fig.228 Price action and momentum divergence signal in MQL5

MQL4

Fig.229 demonstrates the use of the Momentum indicator to build an effective trend reversal trading signal.

Line 38 – 43: Declare variables that store the indicator’s data points. Pay attention to parameter number five in the function iMomentum(). The fifth parameter represents the index of the array element where zero corresponds to the latest data point and one, the previous data point. 

Line 46 – 68: IF statement to find potential price reversal by comparing the Momentum indicator’s last 5 data points with the latest data point with the underlying instrument’s price action. A signal is triggered when the momentum indicator and the price action trend move in the opposite direction.

Fig.229 Price action and momentum divergence signal in MQL4